K - Random Numbers Gym - 101466K ------线段树+DFS序

发表于 | 更新于 | 阅读次数：
本文字数： 7.4k | 阅读时长 ≈ 7 分钟

K. Random Numbers

time limit per test

2.0 s

memory limit per test

256 MB

input

standard input

output

standard output

Tamref love random numbers, but he hates recurrent relations, Tamref thinks that mainstream random generators like the linear congruent generator suck. That’s why he decided to invent his own random generator.

As any reasonable competitive programmer, he loves trees. His generator starts with a tree with numbers on each node. To compute a new random number, he picks a rooted subtree and multiply the values of each node on the subtree. He also needs to compute the number of divisors of the generated number (because of cryptographical applications).

In order to modify the tree (and hence create different numbers on the future), Tamref decided to perform another query: pick a node, and multiply its value by a given number.

Given a initial tree _T_, where _T__u_ corresponds to the value on the node _u_, the operations can be summarized as follows:

  • RAND: Given a node _u_ compute 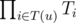and count its divisors, where _T_(_u_) is the set of nodes that belong to the subtree rooted at _u_.

  • SEED: Given a node _u_ and a number _x_, multiply _T__u_ by _x_. Tamref is quite busy trying to prove that his method indeed gives integers uniformly distributed, in the meantime, he wants to test his method with a set of queries, and check which numbers are generated. He wants you to write a program that given the tree, and some queries, prints the generated numbers and count its divisors.

    Tamref has told you that the largest prime factor of both _T__u_ and _x_ is at most the Tamref’s favourite prime: 13. He also told you that the root of _T_ is always node 0.

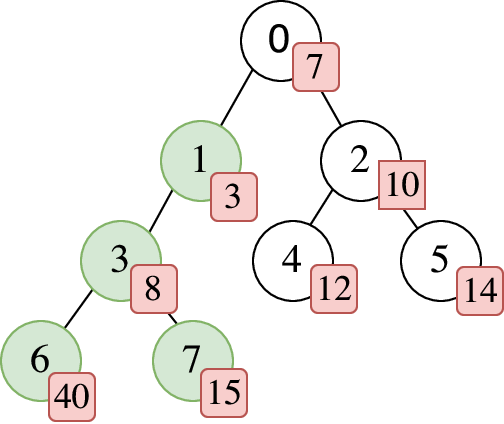
    The figure shows the sample test case. The numbers inside the squares are the values on each node of the tree. The subtree rooted at node 1 is colored. The RAND query for the subtree rooted at node 1 would generate 14400, which has 63 divisors.

    Input

    The first line is an integer _n_ (1 ≤ _n_ ≤ 105), the number of nodes in the tree _T_. Then there are _n_ - 1 lines, each line contains two integers _u_and _v_ (0 ≤ _u_, _v_ < _n_) separated by a single space, it represents that _u_ is a parent of _v_ in _T_. The next line contains _n_ integers, where the _i_ - _th_ integer corresponds to _Ti_ (1 ≤ _Ti_ ≤ 109). The next line contains a number _Q_ (1 ≤ _Q_ ≤ 105), the number of queries. The final _Q_ lines contain a query per line, in the form “_RAND_ _u_” or “SEED _u_ _x_” (0 ≤ _u_ < _n_, 1 ≤ _x_ ≤ 109).

    Output

    For each _RAND_ query, print one line with the generated number and its number of divisors separated by a space. As this number can be very long, the generated number and its divisors must be printed modulo 109 + 7.

    Example

    input

    Copy

1
2
3
4
5
6
7
8
9
10
11
12
13
 8
0 1
0 2
1 3
2 4
2 5
3 6
3 7
7 3 10 8 12 14 40 15
3
RAND 1
SEED 1 13
RAND 1

output

Copy

1
2
 14400 63
187200 126

题意：建一颗树，查询 所有以当前节点和所有儿子节点因子个数，更新，单点更新倍数。

题解：首先dfs把所有位置出现的序 排好。题目样例 dfs,进入的先后顺序 是

s[0]=1,s[1]=2,s[3]=2,s[6]=4,s[7]=5,s[2]=6,s[4]=7,s[5]=8;

然后保留每个节点最后一个所覆盖的最大范围如：

e[0]=8, 因为 0节点覆盖了所有节点也就是 1-8 ，e[1]=5,1节点 覆盖了所有序从 s[1]-e[1]（2 - 5）的节点。

然后以序建一颗线段树：

查询： x 每次查询 [s[x],e[x]];

更新： x 每次更新 [ s[x] ,s[x] ];

我的线段树每次保存的是 (l,r] ,所以 l 每次要-1。

这题数据处理，每个节点保留所有素数因子个数，然后求的值就是所有素数的乘积，因子个数就是相应素数个数+1的乘积，

假如 素因子2有6个，素因子3有 2个 ，素因子5有2个，输出就是 2^63^25^2, 733 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
 #include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<vector>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#include<stack>

using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;

#define bug printf("*********\n");
#define debug(x) cout<<"["<<x<<"]" <<endl;
#define mid (l+r)/2
#define chl 2*k+1
#define chr 2*k+2
#define lson l,mid,chl
#define rson mid,r,chr
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a));

const long long mod=1e9+7;
const int maxn=2e5+5;
const int INF=0x7fffffff;
const int inf=0x3f3f3f3f;
const double eps=1e-8;
vector<int> G[maxn];
int e[maxn],s[maxn];
int val[maxn],val2[maxn];
int cnt=0;
int dfs(int r,int p) {
    cnt++;
//    debug(r);
    val[cnt]=val2[r];
    s[r]=cnt;
    for(int i=0; i<G[r].size(); i++) {
        int to=G[r][i];
        if(to!=p) {
            dfs(to,r);
        }
    }
    e[r]=cnt;
}

int dat[maxn<<4][6];
int prim[]= {2,3,5,7,11,13};
void init(int l,int r,int k) {
    if(r-l==1) {
        for(int i=0; i<6; i++) {
            while(val[r]%prim[i]==0) {
                val[r]/=prim[i];
                dat[k][i]++;
            }
        }
    } else {
        init(lson);
        init(rson);
        for(int i=0; i<6; i++) {
            dat[k][i]=dat[chl][i]+dat[chr][i];
        }
    }
}
void update(int a,int b,int l,int r,int k,ll x) {
    if(b<=l||a>=r) {
        return ;
    } else if(a<=l&&r<=b) {
        for(int i=0; i<6; i++) {
            while(x%prim[i]==0) {
                x/=prim[i];
                dat[k][i]++;
            }
        }
        return ;
    } else {
        update(a,b,lson,x);
        update(a,b,rson,x);
        for(int i=0; i<6; i++) {
            dat[k][i]=dat[chl][i]+dat[chr][i];
        }
    }
}
int res[6];
void query(int a,int b,int l,int r,int k) {
    if(b<=l||a>=r) {
        return ;
    } else if(a<=l&&r<=b) {
        for(int i=0; i<6; i++) {
            res[i]+=dat[k][i];
        }
    } else {
        query(a,b,lson);
        query(a,b,rson);
    }
}
long long pow(long long x,long long n,long long mod=1e9+7) {
    long long res=1;
    while(n>0) {
        if(n&1)res=res*x%mod;
        x=x*x%mod;
        n>>=1;
    }
    return res%mod;
}

int main() {
    int n;
    scanf("%d",&n);
    for(int i=1; i<n; i++) {
        int a,b;
        scanf("%d%d",&a,&b);
        G[a].push_back(b);
        G[b].push_back(a);
    }
    for(int i=0; i<n; i++) {
        scanf("%d",&val2[i]);
    }
    dfs(0,-1);
    init(0,n,0);
    int q;
    scanf("%d",&q);
    while(q--) {
        char ch[100];
        scanf("%s",ch);
        if(ch[0]=='R') {
            int a;
            scanf("%d",&a);
            mem(res,0);
            query(s[a]-1,e[a],0,n,0);
            ll ans=1,num=1;
            for(int i=0; i<6; i++) {
                ans*=pow(prim[i],res[i],mod);
                ans%=mod;
                num*=res[i]+1;
                num%=mod;
            }
            printf("%lld %lld\n",ans%mod,num%mod);
        } else {
            int a;
            ll b;
            scanf("%d%lld",&a,&b);
            update(s[a]-1,s[a],0,n,0,b);
        }
    }
    return 0;
}

0